A. Kaminsky^®

Обоснование термодинамики и статистики

Как учит нас философия, случайность- это непознанная закономерность.
Познавать ее многим лень, поэтому все необычное списывается на случайность!

Фраза с одного из форумов в интернете.

О случайности и закономерности

    Известно, что Н.Бор онтологизировал математическое понятие вероятности. С этим резко не согласился Эйнштейн.   В статье ”Можно ли считать квантовомеханическое описание физической реальности полным?” Эйнштейн утверждал, что волновая механика не полна, и со временем должна появиться более глубокая теория, объясняющая суть квантовых явлений.  Того же мнения придерживался Поль Дирак.  Но, возврат к детерминизму, по мнению Дирака, возможен только ценой существенного пересмотра современной физической парадигмы. Это сопряжено со значительными трудностями и на сегодня не имеет серьезной мотивации. Поэтому, копенгагенская интерпретация КМ, названная так  в честь события 1927 г, когда в совместной работе Нильса Бора и Вернера Гейзенберга в Копенгагене была дана окончательная формулировка квантовой механики стала основной парадигмой физики 20-го столетия. Глубинную неудовлетворенность многих физиков сложившимся положением вещей нельзя объяснить их консерватизмом или неспособностью принять что-то новое...  (Эйнштейн, Дирак, де-Бройль) . Говоря о квантовой механике, И. И. Раби писал: “ ...Мне кажется, что мы упустили ключевой момент”. Мы не знаем имел ли в виду Раби что-то конкретное....

Этим "ключевым моментом" на мой взгляд является неполнота, обусловленная характером субъект-объектных отношений в конечном мире.

Неполнота

Предположим, что мир - конечная система с числом состояний: Nw=Nsubj*Nobj, принадлежащих множеству мировых состояний W.  Nsubj- число состояний субъекта из множества состояний субъекта  SUBJ , Nobj– число состояний объекта (мира без субъекта) из множества состояний объекта OBJ. Это понимание предполагает, что все знания наблюдателя, его опыт и память принадлежат множеству его состояний

SUBJ ÎW.  Тогда, состояния из множества OBJ принципиально не доступны для его восприятия.  Такое  положение вещей мы называем - физической неполнотой. Так возникают два слоя реальности – слой гипотетического внешнего объективного наблюдателя для которого доступно каждое состояние мира и - слой субъективного наблюдателя, которому открыта физическая реальность, в виде структур, образованных его же собственными состояниями. Каждое из которых образует класс  принципиально не различимых (скрытых) состояний мира. В разделе посвященном обоснованию квантовой механики мы показали, что

пространство, построенное над классами  состояний сознания является ни чем иным, как Гильбертовым пространством квантовой механики.  

 Обоснование закона неубывания энтропии. Роль субъекта.

Покажем, что идея  фундаментальной неполноты проливает свет на проблему  закона возрастания энтропии.

Максимально сложным объектом будем называть объект не обладающий функциональной избыточностью.  Это понятие подобно понятию максимально сложной последовательности чисел. По определению, алгоритм генерирующий эту последовательность не может быть проще ее самой. Аналогично, физическим максимально сложным объектом назовем функционально не упрощаемый объект. Легко понять, что максимально сложный объект, будучи замкнутым, не может интерпретировать необратимые алгоритмы. Действительно, для реализации необратимого алгоритма, например, алгоритма сложения чисел, устройство с необходимостью должно рассеивать тепло, которое в случае замкнутой системы может поглощаться избыточными  степенями свободы. Такое устройство будет работать некоторое время - до его естественной "тепловой" смерти. То есть, до тех пор, пока его функциональные степени свободы будут достаточно "холодны". Если же этого избыточного буфера у системы нет, то есть, она максимально сложна, то его интерпретирующие возможности будут ограничены классом обратимых алгоритмов.

Обобщая эти рассуждения, мы можем заключить, что фундаментальная необратимость нашего мира связана с субъектом, разделяющим его на субъективно-функциональные  и некие скрытые буферные степени свободы. Механизм этого разделения обусловлен физической неполнотой, рассмотренной выше. При этом функциональные степени свободы - суть состояния субъекта SUBJ, а избыточная тепловая "баня" - множество состояний OBJ.    

Калибровка Энтропии и субъективная избыточность мира

Наблюдатель всегда может абстрагироваться от внутренней структуры элементов, составляющих систему, положив энтропию каждого из этих элементов равной нулю и опустив тем самым начало отсчета на шкале энтропии до системообразующего (субъективно-функционального) уровня. Именно это позволяет  ему физическую энтропию отождествить с мерой информации.

Абстрагируясь, например, от атомно-молекулярной структуры кремниевых кристаллов, на основе которых построены логические элементы современных компьютеров, энтропия электронного регистра может быть определена, как S=log₂N, где N- число двоичных разрядов регистра. Энтропия же регистра, как физического устройства значительно больше. Она складывается из термодинамической энтропии, а так же из энтропии субатомного уровня составляющих его элементов. Другими словами наблюдатель может условно выбирать точку нуля на шкале энтропии. Важно, однако, то, что он не всегда волен выбирать эту точку по своему усмотрению. Легко понять, что нижняя граница шкалы субъективной энтропии не может быть ниже:

Здесь 1/R=Nw/ Nsubj -степень вырождения физических состояний, определяющая нижнюю границу элементарности материи. Очевидно, что термодинамический нуль энтропии, задаваемый теоремой Нернста лежит выше значения, задаваемого этим выражением. Логарифм этой величины естественно назвать скрытой энтропией:

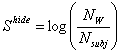
Так как всегда 1/R>0,  мир для субъекта избыточен. Более того, есть основания думать, что  1/R>>0 и это означает, что он "сильно" избыточен.

Проблема энтропии

 Проблемой энтропии в настоящее время называют ряд вопросов из области статистической физики и ее приложений, на которые нет достаточно ясных ответов и которые вряд ли могут быть получены без препарирования столь фундаментальных понятий, как время, обратимость, случай и ряда других.

Исследование этой проблемы в рамках алгоритмической  модели существенно упрощает задачу. Мы надеемся, что изложенный подход сможет упорядочить представление о предмете. В вершине смысловой иерархии различных определений энтропии лежит формула  Шеннона[1]

S=-I=åp_ilogp_i         (1)

которая определяет меру недостаточности информации в сообщении. Если pi определить как удельные веса чистых состояний в некотором смешанном состоянии, то мы приходим к понятию энтропии физической системы:

S=-kår_ilnr_i    (2)

Здесь ρi -диагональный элемент матрицы плотности В замкнутой системе ρi  описывается обратимым во времени  уравнением Лиувилля:

         или   Поэтому     

Другими словами энтропия замкнутой изолированной системы не зависит от времени. Однако, второй закон термодинамики, обобщающий наш опыт в обозримой части вселенной и на известном интервалле времени, свидетельствует об обратном, а именно, о росте энтропии. Множество искусственных толкований этого парадокса создают ощущение  дискомфорта в этой области науки. Встает фундаментальный  вопрос- как может быть обоснован второй закон термодинамики?.

* * *

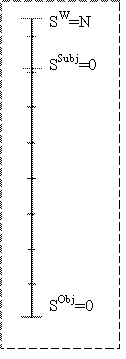
Субъективная перенормировка энтропии

Стрела времени задает направление "процессов жизни" - процессов получения информации, идущих с понижением энтропии. В противоположном направлении идут процессы "забывания" и диссипации.

 Еще в 60-х годах прошлого века профессор Н. И. Кобозев из МГУ обратил внимание на, так называемый, "парадокс мышления". Парадокс состоит в том, что, если референтом процессов мышления являются физические процессы в мозге, то силлогизмам (A=A) должны соответствовать безэнтропийные процессы, которые невозможны при T>0. 

  Субъективная перенормировка энтропии легко разрешает эту проблему. Энтропия ментального мира отлична от физической энтропии. Интуитивно удобной является шкала, нулевое значение которой как раз соответствует силлогизмам.  

Необратимость  порождается наблюдателем

Неполнота накладывает ограничения на возможность субъекта (наблюдателя) различать тонкие структуры материи путем дробления.  Если "разрешающая способность" субъекта R=Nsubj/Nw (величина обратная степени вырождения физических состояний) достаточна чтобы наблюдать за переходами между состояниями, изображенными маленькими кружками (Это могут быть ячейки в фазовом пространстве. (рисунок справа), то для такого наблюдателя процесс обратим. Делая измерение, он не получает новой информации, поскольку уже владеет ею. Он "видит", что условно описываемый здесь распад "частицы" идет по каналу:  4=3+1 и, что это единственная возможность. Если же наблюдатель не способен различить тонкую структуру динамики, то для него существует 3 возможных варианта распада: 4=3+1, 4=2+2 или 4=4+0 , выбрать между которыми он не в состоянии. Только результат  измерения может принести наблюдателю новую информацию о том какой из каналов реализовался,  но он посчитает такое событие чисто случайным. 

 Очевидно, что при реализации операции сложения (умножения) идеальный (максимально сложный) компьютер должен рассеивать тепло в окружающую среду. Как мы уже говорили, эти необратимые процессы невозможно реализовать на фундаментальном уровне. Однако, они могут быть легко реализованы субъектом в  ментальном пространстве его сознания благодаря субъективной избыточности мира.

Мир для наблюдателя, являющегося его частью, как бы обладает избыточностью - кажется таковым, так как, от такого наблюдателя всегда скрыта тонкая структура этого Мира (скрытые степени свободы). В "грубых" же структурах, для которых "тонкие" составляют скрытый тепловой резервуар, возможны необратимые процессы. То есть, наблюдаемые нами в окружающем нас Мире необратимые процессы являются только кажущимся проявлением истинно обратимого Алгоритма, управляющего Миром. Следует ли необратимости, возникающей по столь фундаментальным причинам, присваивать статус кажущейся?. Видимо нет; ибо это - единственная физическая реальность, доступная наблюдателю. 

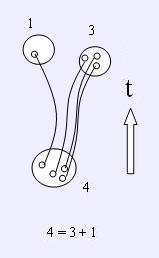
Пример с распадом частицы и измерением можно описать в терминах квантовой механики: 

 |4>= (|3> + |1>).

|Я4>=(|Я1> + |Я3>)

Здесь |4> это состояние системы до измерения, которое при измерении редуцирует в одну из составляющих |3> или |1>. |Я4> это состояние наблюдателя до измерения. Система после измерения находится в запутанном или в квантово-коррелированном состоянии::

|Ψ>=|Я1>|3> + |Я3>|1>

  Мы хотим получить матрицу плотности наблюдателя (наблюдаемые состояния), поэтому свертываем по степеням свободы системы. Формально, энтропия при этом возрастает, так как система переходит в смешанное состояние, описывающееся свернутой по степеням свободы системы матрицей плотности.

Обратите внимание - операция сложения, сама по себе, не обратима, так как разложение суммы на слагаемые не однозначно. Направление движения вперед во времени соответствует в нашем примере разложению на слагаемые. Движение назад во времени равносильно забыванию о том из каких слагаемых составлена сумма.. При этом информация "утекает" в скрытые степени свободы. Утверждается, что квантовый компьютер может работать в унитарном режиме без рассеяния тепла. Однако, здесь не все ясно...

  Мы предполагаем, что наш Мир максимально сложен (то есть, он не обладает избыточностью). Ему некуда рассеивать тепло, и следовательно, алгоритм, управляющий таким миром, должен быть из класса обратимых. Таким образом, на фундаментальном (объективном) уровне, детерминизм и обратимость становятся синонимами. В отличие от этого, как мы показали, в  слое физической (субъективной) реальности, процесс может быть детерминирован, но не обратим. Тому имеется множество примеров - это различные механизмы, как механические, так и электронные. Все они жестко детерминированы, но в процессе работы рассеивают тепло. Диссипация энергии в процессе работы таких механизмов, как может показаться, не является вредным побочным эффектом, а наоборот - необходимым условием их работы (Смотрите заметку о собачке Фейнмана справа). Как же понять этот случай, когда казалось бы в обратимом процессе происходит диссипация энергии? Дело в том, что обратимость таких устройств кажущаяся. Субъективно-детерминистическая эволюция системы имеет место в ментальном пространстве субъекта. Состояния между которыми осуществляются переходы объективно не существуют. Более того, часы, компьютеры и прочие механизмы - виртуальные конструкты нашего сознания.  "работа" этих механизмов, как и самого сознания, возможна исключительно благодаря  априорной неполноте в объективно существующей структуре субъект-объектного отношения.      

Переход к субъектвному наблюдателю, как ренормализационное преобразование (Скейлинг).

Детерминизм на фундаментальном уровне мироустройства приводит к представлению о мире как о некоем конечном автомате с огромным числом внутренних состояний. Динамика такого "мирового" автомата в пространстве его состояний при некоторых условиях может приближаться к дискретному аналогу детерминированного хаоса. Примером простейшей системы, порождающей детерминированный хаос, может служить квадратичное отображение, описывающее динамику популяции в биологической нише  [8]:

Поведение такой системы, как известно, определяется параметром r. При r=r_с→0.892… поведение системы после ряда бифуркаций становится хаотическим. Как будет выглядеть динамика мира для наблюдателя, являющегося частью алгоритмического мира, описывающегося рекурентной формулой приведенной выше?. Для рассматриваемого простого случая на этот вопрос ответить не трудно . Нужно просто принять во внимание тот факт, что наблюдатель занимает часть вычислительных ресурсов (ячеек) мирового автомата. Весьма важным является и понимание того факта, что мы сами вместе с нашей аппаратурой являемся частью мира, в котором живем.  Такому наблюдателю очевидно не могут быть доступны все состояния мира - автомата. "Природа" для него будет представляться значительно более огрубленной, крупнозернистой, чем есть на самом деле. Другими словами, наблюдатель увидит мир ренормализованным. Фрактальный хаос обретет черты некоего порядка. Так, если в нашей модели мир находится вблизи критического состояния  r_с , то после масштабного преобразования, обусловленного переходом к субъективному наблюдателю, значение параметра r уменьшится и мы окажемся в бифуркационной области, где господствует определенный структурный порядок в виде многостадийного цикла.  Возможно, что циклические процессы, начиная с субатомных колебаний и кончая динамикой галактических скоплений, являются следствием нашей ренормализованной субъективной точки зрения. Наблюдаемое фрактальное подобие  мира также подтверждает нашу гипотезу. Этим же решается и трудная проблема низкой начальной энтропии мира, в котором мы живем.

Необратимость и собачка Фейнмана

Эта собачка (а) не лает не кусает, а помогает храповику (b) в механических часах вращаться в одном направлении. Этот замечательный пример, который рассматривает Фейнман в своих знаменитых лекциях непосредственно демонстрирует как в процессе диссипации энергии РОЖДАЕТСЯ ВР ЕМЯ. Не думаете же Вы (я надеюсь), что часами мы измеряем время! Как и любой другой необратимый процесс, часы создают время!  Не будь необратимых процессов мы не замечали бы течение времени.

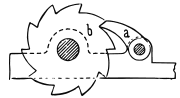
Из субъективной физики следует, что необратимость мира обусловлена исключительно нашей способностью наблюдать, измерять, вычислять. Это по нашей "вине" компьютеры вычисляют, а часы показывают время. Собачка Фейнмана защелкивает "секунды", а не дрожит конвульсивно под действием тепловых флуктуаций, мешая храповику поворачиваться в одном направлении, только потому, что мы способны наблюдать за часами.Если же быть до конца последовательным, то следует заметить, что работа любых сконструированных нами устройств по сути является частью необратимого процесса нашего сознания.

Б.М. Менский так же пришел к субъективности энтропии и стрелы времени. Он пишет:

Объективно существующий квантовый мир - обратим, а необратимость появляется в той картине этого мира, которая возникает в сознании.

УФН, том 177, № 4. Апрель 2007г.

Читать дальше

Обоснование теории относительности

Обоснование квантовой механики